hello_mayesh

Fibonacci Search

Fibonacci Search

Mayesh Mohapatra's photo
Mayesh Mohapatra
·

9 min read

Fibonacci Search is an efficient search algorithm based on the divide and conquer principle. Fibonacci Search works on sorted arrays and uses the Fibonacci Series to determine the index position to be searched in the array. The divide and conquer approach used, helps to narrow down possible locations with the use of Fibonacci numbers.

The fibonacci property says that a number is the sum of its two predecessors, this can be framed into the following recurrence relation

f(K) = f(K-1) +f(K-2)

Therefore, this sequence can be computed by the use of repeated addition. With binary search we divide the seek area in equal parts i.e., a 1:1 ratio, but with fibonacci the ratio of this search area divide could be approaching 1:1.618 while using simpler operations.

Fibonacci Search has a greater advantage when the elements being searched have non-uniform access memory storage(i.e., the time needed to access a storage location varies depending on the location accessed) as it slightly reduces the average time needed to access a storage location. If the machine being used has a direct mapped CPU cache, binary search may lead to more cache misses as the elements that are being accessed often would eventually tend to gather in only a few cache lines, this is tranquilized by splitting the array in parts that do not tend to be powers of two.

(α, β) Fibonacci sequence

The (α, β) Fibonacci sequence could be defined as, given integers α>=1 and β>=1, the (α, β) fibonacci sequence is given by the recurrence relation,

g(k) = g(k − α) + g(k − β)

The (α, β) Fibonacci sequence is actually a family of generalized Fibonacci sequences. We arrive at the classical fibonacci sequence for {α, β} = {1, 2} and initial values f(0) = 0 and f(1) = 1.

The Algorithm

Assume that we have an unsorted array A[] of size n, and we need to find the element 'x'.
Step 1:
Find the smallest Fibonacci number just greater than or equal to the size of array n. Let this number be mth Fibonacci number fib(m) and its predecessor fib(m-1) and fib(m-2). Also, initialize the offset as -1.

Step 2:
While fib(m-2) is greater than 0 do the following:

  • Compare X with the last element covered by fib(m-2). It is given by A[min(offset + fib(m-2), n - 1)].
  • If X equals this element, then return the index.
  • Else if X is smaller than this element, we discard the half after this element and move the Fibonacci sequence two steps backward. Also, update the offset to change the starting index of search space. These steps discard the rear two-third of the array search space.
  • Else if X is greater than this element, we discard the half before this element and move the Fibonacci sequence one step backward. This step discards the front one-third of the array search space.

Step 3:
If fib(m-1) equals 1 we have one element left unchecked, compare it with X. If X equals this element then return the index.

Step 4:
If none of the elements matched, return -1.

Implementation

The pythonic implementation of the above described algorithm is as follows,

def FibonacciSearch(lys, val):
    fibM_minus_2 = 0
    fibM_minus_1 = 1
    fibM = fibM_minus_1 + fibM_minus_2
    while (fibM < len(lys)):
        fibM_minus_2 = fibM_minus_1
        fibM_minus_1 = fibM
        fibM = fibM_minus_1 + fibM_minus_2
    index = -1;
    while (fibM > 1):
        i = min(index + fibM_minus_2, (len(lys)-1))
        if (lys[i] < val):
            fibM = fibM_minus_1
            fibM_minus_1 = fibM_minus_2
            fibM_minus_2 = fibM - fibM_minus_1
            index = i
        elif (lys[i] > val):
            fibM = fibM_minus_2
            fibM_minus_1 = fibM_minus_1 - fibM_minus_2
            fibM_minus_2 = fibM - fibM_minus_1
        else :
            return i
    if(fibM_minus_1 and index < (len(lys)-1) and lys[index+1] == val):
        return index+1;
    return -1

A step-by-step process of this search would be,
We put in the following as the inputs to the function
lys = [1,2,3,4,5,6,7,8,9,10,11]
val = 6

  • Determine the smallest fibonacci number greater than or equal to the length. In this case we would end up with the value of 13. So,
    fibM = 13
    fibM_minus_1 = 8
    fibM_minus_2 = 5
    index = -1
  • Now, we go on to check lys[4] where 4 is the minimum of -1+5. As element at lys[4] is smaller than the value we need, we move the fibonacci numbers one step down in the sequence. Now the values are updated as follows,
    fibM = 8
    fibM_minus_1 = 5
    fibM_minus_2 = 3
    index = 4
  • Next, we check the element at index 7, i.e., lys[7], the element at this index is 8, greater than the value we are searching for, we now move the fibonacci numbers two steps down in the sequence.
    fibM = 3
    fibM_minus_1 = 2
    fibM_minus_2 = 1
    index = 4
  • Next, we check the element at lys[5], the value of which is 6 which is the value we have been looking for. Now we can return this result.

With fibonacci search the sub arrays formed are of sizes which are two consecutive fibonacci numbers. This may lead to about 4% more comparisons to be executed, but it has the advantage that there is only addition and subtraction involved to calculate the indices of the accessed array elements, whereas in the case of a classical binary search problem, to access array elements the operations that were needed are bit-shifts, multiplication or division, these however were less common at the time when fibonacci search was first introduced. With fibonacci search elements being examined are relatively closer elements in subsequent steps. So when the input array is big enough that it cannot fit in CPU cache or even in RAM, fibonacci search can be useful.

Time Complexity

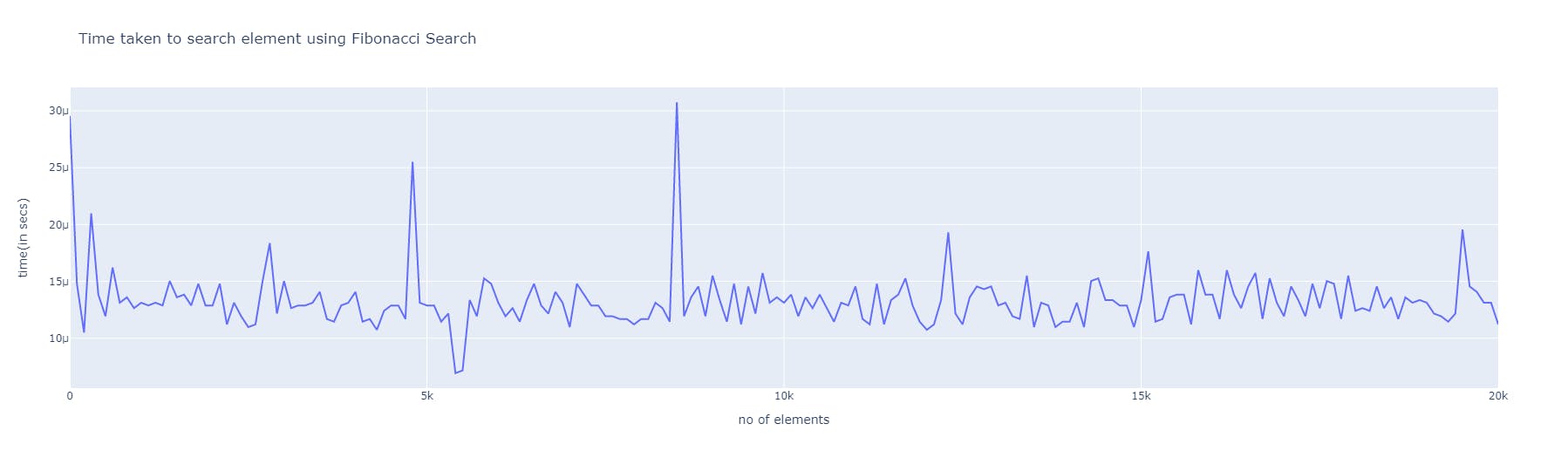
newplot (3).png

Average Case

We bring down the search space by approximately one-thirds/two-third as we iterate, which would bring the complexity to logarithmic. So the average case time complexity of the fibonacci search algorithm would be O(logn).

Best Case

In the best case, the element to be searched is the first to be compared. So the best case complexity would be O(1).

Worst Case

The worst case would occur when the element to be searched is always present in the larger subarray and would require the complete traversal. The worst case time complexity would be O(logn).

Space Complexity

Fibonacci Search doesn't require any additional space other than temporary variables. So the Space Complexity of fibonacci search would be constant i.e., it would be O(1).

References

algorithmsdata structuresPython 3C++General Programming